The Hubble Constant
In Julius Caesar William Shakespeare wrote “But I am constant as the Northern Star, of whose true and resting quality there is no fellow in the firmament.” However, had he known about cosmology, he’d have probably chosen a better comparison than Polaris, which is actually a variable star.
Stars like Polaris, called Cepheid variables, have a wonderful property (wonderful to astronomers, that is). The rate at which they pulsate is simply related to their luminosity. So, by observing the apparent brightness of a Cepheid and its period of variability it is straightforward to estimate its distance. Because astronomers can measure the distance to Cepheids — and, thus, to the galaxies they inhabit — these peculiar stars hold the key to many important questions in Cosmology.
NASA Scientists announced that they had used the Hubble Space Telescope to study Cepheid variables and measure the expansion of the Universe with unprecedented precision. To fully grasp the meaning of these new measurements it may help to reflect on events 70 years ago, when a young American astronomer named Edwin Hubble was using the great telescopes of his day to study the large-scale structure of the Universe.
In 1929, as Hubble pursued his studies of distant galaxies, he realized something extraordinary. Ten years earlier Shapley had noticed that other galaxies appeared to be flying away from our own Milky Way. Hubble had the insight to realize that not only were these objects apparently speeding away, but the farther away they were, the faster they appeared to be moving. Thus the Hubble Constant, Ho, was born. Ho is a number which relates a galaxy’s apparent speed of recession to its distance from the Milky Way, as shown in the graph below.
Scientists now know that the observed recessional velocites are not distant galaxies flying through space, all away from the Milky Way, but instead are actually a result of the expansion of the Universe itself (and everything in it). This expansion would look the same no matter what galaxy we actually inhabited, and is one of the visible pieces of evidence that points to a “Big Bang” origin for our Universe.

The Hubble Constant describes how fast objects appear to be moving away from our galaxy as a function of distance. If you plot apparent recessional velocity against distance, as in the figure above, the Hubble Constant is simply the slope of a straight line through the data.
The Hubble Constant is usually expressed in units of “kilometers per second, per Megaparsec.” One parsec is a unit of distance equal to about 3.2 light years, and a Megaparsec is a million times this, or about 3.2 million light years. So what the Hubble Constant says is that for every 3.2 million light years you look out into space, the objects there appear to be receding from you at a rate of Ho kilometers per second. If Ho is 100, then the objects appear to recede at 100 km/second for every 3.2 million light years you look out into space. If Ho is 50, then you have to look about 6.4 million light years out into space for the same 100 km/second recessional velocity.
But how do astronomers measure Ho in the absence of a cosmic “radar gun” and mile-markers? There are actually several ways, each with their own advantages, disadvantages, and sources of uncertainty. Some involve the study of supernovae with optical telescopes, others capitalize on a physical process in distant clusters of galaxies called the Sunyaev-Zeldovich effect that can be detected by combining X-ray images and microwave astronomy measurements. Another method, used by scientists working with the Hubble Space Telescope, for example, involves looking at “Cepheid Variables” in distant galaxies.
Cepheids (named as a group after the star delta-Cephei) have been known for quite awhile, and they exhibit a very regular fluctuation in their brightness on timescales of about 2 to 100 days. Polaris, the “North Star” is indeed a member of this class of variables. It turns out that the frequency with which they change their brightness is directly related to the star’s intrinsic luminosity. This so-called “Period-luminosity relationship” was discovered by Henrietta Levitt, an astronomer who worked at Harvard in the early decades of this century.
For nearby Cepheids that can easily be resolved in ground-based telescopes, it is fairly easy to measure both the brightness and the period of the star. With these measurements in hand, by using the period-luminosity relationship, one can find the luminosity of the star. And since the luminosity and brightness are related by an inverse-square law, the distance to the star can be determined with a bit of simple 7th or 8th-grade algebra. This works great for stars within our galaxy, and in some nearby galaxies like M31 (Andromeda) and M33. Indeed Hubble himself put the question of “the realm of the nebulae” to bed in 1923 by measuring Cepheids in these galaxies, and deducing a distance of about 900,000 light years. This distance was at least a factor of 20 or more farther than any object within our galaxy, showing that these nebulae were indeed galaxies in their own right, rather than collections of stars, gas, and dust within our own Milky Way.
But on cosmological scales, 900,000 light years is the equivalent of a local phone call. At these nearby distances, the cosmological expansion proceeds very slowly (two dots near each other on the surface of the balloon experiment above hardly move with respect to one another) with velocities equal to or less than typical random motions of stars within the galaxy, more like the velocity of the Earth around the Sun, about 30 km/second or less.
Going deeper into space, where the expansion proceeds more rapidly, to look at individual Cepheids was a difficult task for most ground based telescopes. So until the Hubble Telescope came along, with its ability to resolve Cepheids in extremely distant galaxies, astronomers had to be a bit more resourceful in getting at the Hubble Constant.
And resourceful they were. Using a variety of methods, many fraught with uncertainty and large systemtic errors, the answers have traditionally come out somewhere between 50 km/s/Mpc and 100 km/s/Mpc. And therein lies the rub. In this difference between 50 and 100 km/s/Mpc lies the fate of the entire Universe.
Ten+1 measurements of the Hubble Constant
| Method Used | Citation | Value (km/second/Megaparsec) |
|---|---|---|
| Cepheid variables in distant galaxies | W. Freedman et al (1999) | 70 +/- 7 |
| M101 group velocity and distance | Sandage and Tammann (1974) | 55.5 +/- 8.7 |
| Virgo Cluster | Peebles (1977) | 42 – 77 |
| Globular Clusters | Hanes (1979) | 80 +/- 11 |
| Virgo Sc HII luminosities | Kennicutt (1981) | 55 |
| Type I supernovae | Branch (1979) | 56 +/- 15 |
| Type I supernovae | Sandage and Tammann (1982) | 50 +/- 7 |
| Infrared Tully-Fisher relation | Aaronson and Mould (1983) | 82 +/- 10 |
| SN-Ia and Cepheids | Sandage, et al. (1994) | 55 +/- 8 |
| 80 +/- 17 | ||
| 90 +/- 10 |
The fate of the Universe actually depends on four numbers, which have been described as the “Holy Grail of Cosmology.” Three of these numbers are independent, meaning if you find three, the fourth one can be computed from the three you know. Among these numbers is the Hubble Constant.
The first number is called the “deceleration parameter,” and it is a measure of how fast the cosmological expansion is speeding up or slowing down. Or, colloquially, does the Universe have it’s foot on the gas or on the brake? Written by scientists as qo (“q-naught”), a positive value of the deceleration parameter means the universe is slowing down (foot on the brake), a value of 0 means the universe is expanding at a constant speed (coasting), and a negative value means that the universe is accelerating (foot on the gas).
The second number is the “density parameter.” Called either `omega’ or `sigma,’ depending on the units one uses, this number describes how much “stuff” is in the universe. The larger the density parameter, the more stuff there is. Issues related to “missing mass” are often tied up in measurements of the density parameter that turn out to be smaller than one needs to theoretically halt the expansion, for example through the self-gravitation of all objects in the Universe.
The third number is simply the age of the universe. How old is this place? We can actually get a decent handle on lower-limits to this number simply by recognizing that the universe has to be older than the oldest objects in it. Radioactive isotope studies yield ages of at least nine to sixteen billion years for our Galaxy, and the ages of the oldest star clusters put the limit at about 14 billion years. Give or take a billion years, a reasonable lower limit to the age of the Universe turns out to be about 15 billion years.
The fourth number is our Hubble Constant Ho. Two other numbers that are often discussed in cosmology, the “cosmological constant,” which Einstein referred to as one of his greatest blunders, and the “curvature of the Universe,” are determined by the density parameter and the deceleration parameter.
The way these numbers play together mathematically allows one to write the product of Ho and the age of the universe as some function of the density parameter and the deceleration parameter.
(Age of the Universe) x (Hubble Constant) = A complicated function of the density and deceleration parameters
In other words, given our fairly robust limit of the age of the Universe, and a reliable measurement of the Hubble Constant, their product restricts our Universe to only a very limited set of combinations of density parameter and deceleration parameter, many of which can be further ruled out by other independent observations. Conversely, if one assumes a cosmological model (i.e. values for sigmao and qo), a measure of the Hubble Constant can give you a measure of the age of the universe.
Regardless of the approach, by getting a reliable measurement of the Hubble Constant, we therefore have a much greater understanding of the nature and eventual fate of the Universe. If the Hubble Constant is large enough, for example, for a given age of the Universe, the deceleration parameter must be negative, meaning that the Universe is not slowing down, but instead is accelerating its expansion.
One can actually draw a “map” of where our Universe might be within the realm of all possibilities, to see these implications of a measurement of Ho. Using the `sigma-q’ notation, it looks something like the accompanying figure.
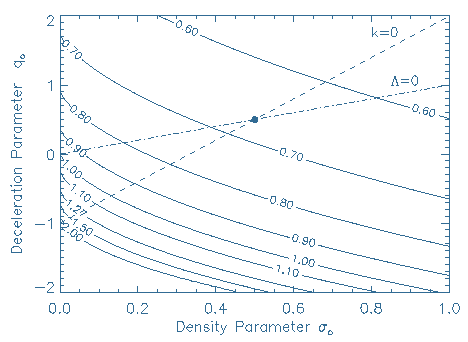
The density parameter `sigmao’ is plotted on the horizontal axis, and the deceleration parameter `qo’ is plotted on the vertical axis. High-density, rapidly decelerating universes are represented at the upper right part of the diagram, and rapidly accelerating, low-density universes are at the lower left. The diagonal dot-dashed line that runs from the origin (0,0) upwards to the right represents universes where the cosmological constant (lambda) is zero (sigmao = qo). Below this line, the cosmological constant is positive, above it, it’s negative. The second diagonal line, dashed-only, delineates the universes that have flat topology (k = 3 sigmao – qo – 1 = 0).
The curves from upper left to lower right are the locus of points where the Hubble Constant times the age of the Universe equals some number, indicated on the line. For example, the Einstein-deSitter model located at the bold dot (sigmao = qo = 1/2) has a value of Ho times the age of the universe equal to 2/3. By measuring the Hubble Constant and multiplying by the age of the Universe, we are restricted to live on one of these curves.
We are somewhere on this diagram…but where?
A value of Ho = 70 km/second/Mpc in an Einstein-de Sitter Universe results in an age of the universe slightly less than 10 billion years, and with the uncertainty in Ho, a value of about 12 billion years is likely not out of the question for this model.
With an age of 15 billion years, consistent with the ages of the oldest star clusters, and a Hubble Constant measurement of 70 km/s/Mpc, one obtains a product of 1.07 (when the units are accounted correctly). This, combined with a strong theoretical impetus for a flat topology (k = 0), would confine our position to a narrow area in the lower left of the diagram, with a positive cosmological constant.
It is indeed possible that our latest measurements of the Hubble Constant may have shown us that our universe is accelerating, and will continue to do so forever. Nature appears to have its foot on the cosmological gas pedal – and we’re along for the ride.
The Einstein-deSitter Universe
The dot located at sigmao=qo=0.5 in the accompanying diagram is the so-called “Einstein de Sitter” universe. It is unique in the sense that it is the only universe that possesses flat topology, and has a zero cosmological constant.
Mathematically, it is much easier to treat as well, as many of the equations can be done by hand in this unique case. The model has been a favorite of scientists for aesthetic, theoretical, and other reasons.
If one assumes that this model is indeed the one that describes our Universe, large measurements of the Hubble Constant can result in an age of the Universe that is younger than the objects we know are in it, an obvious impossibility.
In such a case, either the model is not the correct one, or the measurement of Ho is in error.

