About Temperature
This document was prepared for the middle school math teachers who are taking part in Project Skymath. It is also hoped that the general public will find it interesting
What is Temperature?
In a qualitative manner, we can describe the temperature of an object as that which determines the sensation of warmth or coldness felt from contact with it.
It is easy to demonstrate that when two objectsof the same material are placed together (physicists say when they are put in thermal contact), the object with the higher temperature cools while the cooler object becomes warmer until a point is reached after which no more change occurs, and to our senses, they feel the same. When the thermal changes have stopped, we say that the two objects (physicists define them more rigorously as systems) are in thermal equilibrium . We can then define the temperature of the system by saying that the temperature is that quantity which is the same for both systems when they are in thermal equilibrium.
If we experiment further with more than two systems, we find that many systems can be brought into thermal equilibrium with each other; thermal equilibrium does not depend on the kind of object used. Put more precisely,
if two systems are separately in thermal equilibrium with a third, then they must also be in thermal equilibrium with each other, and they all have the same temperature regardless of the kind of systems they are.
The statement in italics, called the zeroth law of thermodynamics may be restated as follows:
If three or more systems are in thermal contact with each other and all in equilibrium together, then any two taken separately are in equilibrium with one another. (quote from T. J. Quinn’s monograph Temperature)
Now one of the three systems could be an instrument calibrated to measure the temperature – i.e. a thermometer. When a calibrated thermometer is put in thermal contact with a system and reaches thermal equilibrium, we then have a quantitative measure of the temperature of the system. For example, a mercury-in-glass clinical thermometer is put under the tongue of a patient and allowed to reach thermal equilibrium in the patient’s mouth – we then see by how much the silvery mercury has expanded in the stem and read the scale of the thermometer to find the patient’s temperature.
What is a Thermometer?
A thermometer is an instrument that measures the temperature of a system in a quantitative way. The easiest way to do this is to find a substance having a property that changes in a regular way with its temperature. The most direct ‘regular’ way is a linear one:
t(x) = ax + b,
where t is the temperature of the substance and changes as the property x of the substance changes. The constants a and b depend on the substance used and may be evaluated by specifying two temperature points on the scale, such as 32° for the freezing point of water and 212° for its boiling point.
For example, the element mercury is liquid in the temperature range of -38.9° C to 356.7° C (we’ll discuss the Celsius ° C scale later). As a liquid, mercury expands as it gets warmer, its expansion rate is linear and can be accurately calibrated.
The mercury-in-glass thermometer illustrated in the above figure contains a bulb filled with mercury that is allowed to expand into a capillary. Its rate of expansion is calibrated on the glass scale.
The Development of Thermometers and Temperature Scales
The historical highlights in the development of thermometers and their scales given here are based on “Temperature” by T. J. Quinn and “Heat” by James M. Cork.
One of the first attempts to make a standard temperature scale occurred about AD 170, when Galen, in his medical writings, proposed a standard “neutral” temperature made up of equal quantities of boiling water and ice; on either side of this temperature were four degrees of heat and four degrees of cold, respectively.
The earliest devices used to measure the temperature were called thermoscopes.
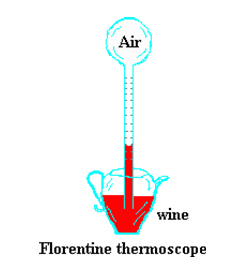
They consisted of a glass bulb having a long tube extending downward into a container of colored water, although Galileo in 1610 is supposed to have used wine. Some of the air in the bulb was expelled before placing it in the liquid, causing the liquid to rise into the tube. As the remaining air in the bulb was heated or cooled, the level of the liquid in the tube would vary reflecting the change in the air temperature. An engraved scale on the tube allowed for a quantitative measure of the fluctuations.
The air in the bulb is referred to as the thermometric medium, i.e. the medium whose property changes with temperature.
In 1641, the first sealed thermometer that used liquid rather than air as the thermometric medium was developed for Ferdinand II, Grand Duke of Tuscany. His thermometer used a sealed alcohol-in-glass device, with 50 “degree” marks on its stem but no “fixed point” was used to zero the scale. These were referred to as “spirit” thermometers.
Robert Hook, Curator of the Royal Society, in 1664 used a red dye in the alcohol . His scale, for which every degree represented an equal increment of volume equivalent to about 1/500 part of the volume of the thermometer liquid, needed only one fixed point. He selected the freezing point of water. By scaling it in this way, Hook showed that a standard scale could be established for thermometers of a variety of sizes. Hook’s original thermometer became known as the standard of Gresham College and was used by the Royal Society until 1709. (The first intelligible meteorological records used this scale).
In 1702, the astronomer Ole Roemer of Copenhagen based his scale upon two fixed points: snow (or crushed ice) and the boiling point of water, and he recorded the daily temperatures at Copenhagen in 1708- 1709 with this thermometer.
It was in 1724 that Gabriel Fahrenheit, an instrument maker of Däanzig and Amsterdam, used mercury as the thermometric liquid. Mercury’s thermal expansion is large and fairly uniform, it does not adhere to the glass, and it remains a liquid over a wide range of temperatures. Its silvery appearance makes it easy to read.
Fahrenheit described how he calibrated the scale of his mercury thermometer:
“placing the thermometer in a mixture of sal ammoniac or sea salt, ice, and water a point on the scale will be found which is denoted as zero. A second point is obtained if the same mixture is used without salt. Denote this position as 30. A third point, designated as 96, is obtained if the thermometer is placed in the mouth so as to acquire the heat of a healthy man.” (D. G. Fahrenheit,Phil. Trans. (London) 33, 78, 1724)
On this scale, Fahrenheit measured the boiling point of water to be 212. Later he adjusted the freezing point of water to 32 so that the interval between the boiling and freezing points of water could be represented by the more rational number 180. Temperatures measured on this scale are designated as degrees Fahrenheit (° F).
In 1745, Carolus Linnaeus of Upsula, Sweden, described a scale in which the freezing point of water was zero, and the boiling point 100, making it a centigrade (one hundred steps) scale. Anders Celsius (1701-1744) used the reverse scale in which 100 represented the freezing point and zero the boiling point of water, still, of course, with 100 degrees between the two defining points.
In 1948 use of the Centigrade scale was dropped in favor of a new scale using degrees Celsius (° C). The Celsius scale is defined by the following two items that will be discussed later in this essay:
(i) the triple point of water is defined to be 0.01 C
(ii) a degree Celsius equals the same temperature change as a degree on the ideal-gas scale.
On the Celsius scale the boiling point of water at standard atmospheric pressure is 99.975 C in contrast to the 100 degrees defined by the Centigrade scale.
To convert from Celsius to Fahrenheit: multiply by 1.8 and add 32.
° F = 1.8° C + 32
(Or, you can get someone else to do it for you!)
In 1780, J. A. C. Charles, a French physician, showed that for the same increase in temperature, all gases exhibited the same increase in volume. Because the expansion coefficient of gases is so very nearly the same, it is possible to establish a temperature scale based on a single fixed point rather than the two fixed- point scales, such as the Fahrenheit and Celsius scales. This brings us back to a thermometer that uses a gas as the thermometric medium.
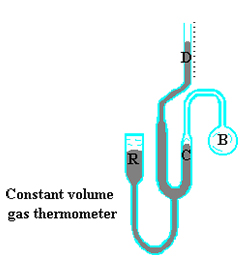
In a constant volume gas thermometer a large bulb B of gas, hydrogen for example, under a set pressure connects with a mercury-filled “manometer” by means of a tube of very small volume. (The Bulb B is the temperature-sensing portion and should contain almost all of the hydrogen). The level of mercury at C may be adjusted by raising or lowering the mercury reservoir R. The pressure of the hydrogen gas, which is the “x” variable in the linear relation with temperature, is the difference between the levels D and C plus the pressure above D.
P. Chappuis in 1887 conducted extensive studies of gas thermometers with constant pressure or with constant volume using hydrogen, nitrogen, and carbon dioxide as the thermometric medium. Based on his results, the Comité International des Poids et Mesures adopted the constant-volume hydrogen scale based on fixed points at the ice point (0° C) and the steam point (100° C) as the practical scale for international meteorology.
Experiments with gas thermometers have shown that there is very little difference in the temperature scale for different gases. Thus, it is possible to set up a temperature scale that is independent of the thermometric medium if it is a gas at low pressure. In this case, all gases behave like an “Ideal Gas” and have a very simple relation between their pressure, volume, and temperature: pV= (constant)T.
This temperature is called the thermodynamic temperature and is now accepted as the fundamental measure of temperature. Note that there is a naturally-defined zero on this scale – it is the point at which the pressure of an ideal gas is zero, making the temperature also zero. We will continue a discussion of “absolute zero” in a later section. With this as one point on the scale, only one other fixed point need be defined. In 1933, the International Committee of Weights and Measures adopted this fixed point as the triple point of water , the temperature at which water, ice, and water vapor coexist in equilibrium); its value is set as 273.16. The unit of temperature on this scale is called the kelvin, after Lord Kelvin (William Thompson), 1824-1907, and its symbol is K (no degree symbol used).
convert from Celsius to Kelvin, add 273.
K = ° C + 273.
Thermodynamic temperature is the fundamental temperature; its unit is the kelvin which is defined as the fraction 1/273.16 of the thermodynamic temperature of the triple point of water.
Sir William Siemens, in 1871, proposed a thermometer whose thermometric medium is a metallic conductor whose resistance changes with temperature. The element platinum does not oxidize at high temperatures and has a relatively uniform change in resistance with temperature over a large range. The Platinum Resistance Thermometer is now widely used as a thermoelectric thermometer and covers the temperature range from about -260° C to 1235° C.
Several temperatures were adopted as Primary reference points so as to define the International Practical Temperature Scale of 1968. The International Temperature Scale of 1990 was adopted by the International Committee of Weights and Measures at its meeting in 1989. Between 0.65K and 5.0K, the temperature is defined in terms of the vapor pressure – temperature relations of the isotopes of helium. Between 3.0K and the triple point of neon (24.5561K) the temperature is defined by means of a helium gas thermometer. Between the triple point of hydrogen (13.8033K) and the freezing point of silver (961.78° C) the temperature is defined by means of platinum resistance thermometers. Above the freezing point of silver the temperature is defined in terms of the Planck radiation law.
T. J. Seebeck, in 1826, discovered that when wires of different metals are fused at one end and heated, a current flows from one to the other. The electromotive force generated can be quantitatively related to the temperature and hence, the system can be used as a thermometer – known as a thermocouple. The thermocouple is used in industry and many different metals are used – platinum and platinum/rhodium, nickel-chromium and nickel-aluminum, for example. The National Institute of Standards and Technology (NIST) maintains databases for standardizing thermometers.
For the measurement of very low temperatures, the magnetic susceptibility of a paramagnetic substance is used as the thermometric physical quantity. For some substances, the magnetic susceptibility varies inversely as the temperature. Crystals such as cerrous magnesium nitrate and chromic potassium alum have been used to measure temperatures down to 0.05 K; these crystals are calibrated in the liquid helium range. This diagram and the last illustration in this text were taken from the Low Temperature Laboratory, Helsinki University of Technology’s picture archive. For these very low, and even lower, temperatures, the thermometer is also the mechanism for cooling. Several low-temperature laboratories conduct interesting applied and theoretical research on how to reach the lowest possible temperatures and how work at these temperatures may find application.
Heat and Thermodynamics
Prior to the 19th century, it was believed that the sense of how hot or cold an object felt was determined by how much “heat” it contained. Heat was envisioned as a liquid that flowed from a hotter to a colder object; this weightless fluid was called “caloric”, and until the writings of Joseph Black (1728-1799), no distinction was made between heat and temperature. Black distinguished between the quantity (caloric) and the intensity (temperature) of heat.
Benjamin Thomson, Count Rumford, published a paper in 1798 entitled “an Inquiry Concerning the Source of Heat which is Excited by Friction”. Rumford had noticed the large amount of heat generated when a cannon was drilled. He doubted that a material substance was flowing into the cannon and concluded “it appears to me to be extremely difficult if not impossible to form any distinct idea of anything capable of being excited and communicated in the manner the heat was excited and communicated in these experiments except motion.”
But it was not until J. P. Joule published a definitive paper in 1847 that the the caloric idea was abandoned. Joule conclusively showed that heat was a form of energy. As a result of the experiments of Rumford, Joule, and others, it was demonstrated (explicitly stated by Helmholtz in 1847), that the various forms of energy can be transformed one into another.
When heat is transformed into any other form of energy, or when other forms of energy are transformed into heat, the total amount of energy (heat plus other forms) in the system is constant.
This is the first law of thermodynamics, the conservation of energy. To express it another way: it is in no way possible either by mechanical, thermal, chemical, or other means, to obtain a perpetual motion machine; i.e., one that creates its own energy (except in the fantasy world of Maurits Escher’s “Waterfall”!)
A second statement may also be made about how machines operate. A steam engine uses a source of heat to produce work. Is it possible to completely convert the heat energy into work, making it a 100% efficient machine? The answer is to be found in the second law of thermodynamics:
No cyclic machine can convert heat energy wholly into other forms of energy. It is not possible to construct a cyclic machine that does nothing but withdraw heat energy and convert it into mechanical energy.
The second law of thermodynamics implies the irreversibility of certain processes – that of converting all heat into mechanical energy, although it is possible to have a cyclic machine that does nothing but convert mechanical energy into heat!
Sadi Carnot (1796-1832) conducted theoretical studies of the efficiencies of heat engines (a machine which converts some of its heat into useful work). He was trying to model the most efficient heat engine possible. His theoretical work provided the basis for practical improvements in the steam engine and also laid the foundations of thermodynamics. He described an ideal engine, called the Carnot engine, that is the most efficient way an engine can be constructed. He showed that the efficiency of such an engine is given by
efficiency = 1 – T”/T’,
where the temperatures, T’ and T” , are the hot and cold “reservoirs” , respectively, between which the machine operates. On this temperature scale, a heat engine whose coldest reservoir is zero degrees would operate with 100% efficiency. This is one definition of absolute zero, and it can be shown to be identical to the absolute zero we discussed previously. The temperature scale is called the absolute, the thermodynamic , or the kelvin scale.
The way that the gas temperature scale and the thermodynamic temperature scale are shown to be identical is based on the microscopic interpretation of temperature, which postulates that the macroscopic measurable quantity called temperature is a result of the random motions of the microscopic particles that make up a system.
This brief summary is abridged from a more detailed discussion to be found in Quinn’s “Temperature”
About the same time that thermodynamics was evolving, James Clerk Maxwell (1831-1879) and Ludwig Boltzmann (1844-1906) developed a theory describing the way molecules moved – molecular dynamics. The molecules that make up a perfect gas move about, colliding with each other like billiard balls and bouncing off the surface of the container holding the gas. The energy associated with motion is called Kinetic Energy and this kinetic approach to the behavior of ideal gases led to an interpretation of the concept of temperature on a microscopic scale.
The amount of kinetic energy each molecule has is a function of its velocity; for the large number of molecules in a gas (even at low pressure), there should be a range of velocities at any instant of time. The magnitude of the velocities of the various particles should vary greatly – no two particles should be expected to have the exact same velocity. Some may be moving very fast; others, quite slowly. Maxwell found that he could represent the distribution of velocities statistically by a function known as the Maxwellian distribution. The collisions of the molecules with their container gives rise to the pressure of the gas. By considering the average force exerted by the molecular collisions on the wall, Boltzmann was able to show that the average kinetic energy of the molecules was directly comparable to the measured pressure, and the greater the average kinetic energy, the greater the pressure. From Boyles’ Law, we know that the pressure is directly proportional to the temperature, therefore, it was shown that the kinetic energy of the molecules related directly to the temperature of the gas. A simple relation holds for this:
average kinetic energy of molecules=3kT/2,
where k is the Boltzmann constant. Temperature is a measure of the energy of thermal motion and, at a temperature of zero, the energy reaches a minimum (quantum mechanically, the zero-point motion remains at 0 K).
In July, 1995, physicists in Boulder, Colo.achieved a temperature far lower than has ever been produced before and created an entirely new state of matter predicted decades ago by Albert Einstein and Satyendra Nath BoseA/a>. The press release describes the nature of this experiment and a full description of this phenomenon is described by the University of Colorado’s BEC Homepage.
Dealing with a system which contained huge numbers of molecules requires a statistical approach to the problem. About 1902, J. W. Gibbs (1839-1903) introduced statistical mechanics with which he demonstrated how average values of the properties of a system could be predicted from an analysis of the most probable values of these properties found from a large number of identical systems (called an ensemble). Again, in the statistical mechanical interpretation of thermodynamics, the key parameter is identified with a temperature which can be directly linked to the thermodynamic temperature, with the temperature of Maxwell’s distribution, and with the perfect gas law.
Temperature becomes a quantity definable either in terms of macroscopic thermodynamic quantities such as heat and work, or, with equal validity and identical results, in terms of a quantity which characterized the energy distribution among the particles in a system. (Quinn, “Temperature”)
With this understanding of the concept of temperature, it is possible to explain how heat (thermal energy) flows from one body to another. Thermal energy is carried by the molecules in the form of their motions and some of it, through molecular collisions, is transferred to molecules of a second object when put in contact with it. This mechanism for transferring thermal energy by contact is called conduction.
A second mechanism of heat transport is illustrated by a pot of water set to boil on a stove – hotter water closest to the flame will rise to mix with cooler water near the top of the pot. Convection involves the bodily movement of the more energetic molecules in a liquid or gas.
The third way that heat energy can be transferred from one body to another is by radiation; this is the way that the sun warms the earth. The radiation flows from the sun to the earth, where some of it is absorbed, heating the surface.
A major dilemma in physics since the time of Newton was how to explain the nature of this radiation.
Thermal Radiation
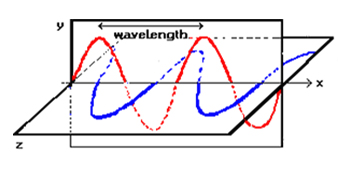
The nature of radiation has puzzled scientists for centuries. Maxwell proposed that this form of energy travels as a vibratory electric and magnetic disturbance through space in a direction perpendicular to those disturbances.
In the diagram, the electric (red) and magnetic (blue) oscillations are orthogonal to each other – the electric lying in the xy plane; the magnetic, in the xz plane. The wave is traveling in the x direction. An electromagnetic wave can be defined in terms of the frequency of its oscillation, designated by the Greek letter nu (v). The wave moves in a straight line with with a constant speed (designated as c if it is moving through a vacuum); the distance between successive ‘peaks’ of the wave is the wavelength,,of the wave and is equal to its speed divided by its frequency.
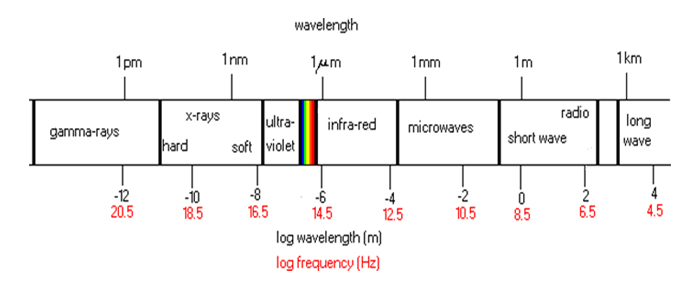
The electromagnetic spectrum covers an enormous range in wavelengths, from very short waves to very long ones.
The only region of the electromagnetic spectrum to which our eye is sensitive is the “visible” range identified in the diagram by the rainbow colors.
The sun is not the only object that provides radiant energy; any object whose temperature is greater than 0 K will emit some radiant energy. The challenge to scientists was to show how this radiant energy is related to the temperature of the object.
If an object is placed in a container whose walls are at a uniform temperature, we expect the object to come into thermal equilibrium with the walls of the enclosure and the object should emit radiant energy just like the walls of the container. Such an object absorbs and radiates the same amount of energy. Now a blackened surface absorbs all radiation incident upon it and it must radiate in the same manner if it is in thermal equilibrium. Equilibrium thermal radiation is therefore called black body radiation.
The first relation between temperature and radiant energy was deduced by J. Stefan in 1884 and theoretically explained by Boltzmann about the same time. It states:
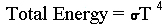
where the total energy is per unit area per second emitted by the back body, T is its absolute (thermodynamic) temperature and is the Stefan-Boltzmann constant.
The great question at the turn of the century was to explain the way this total radiant energy emitted by a black body was spread out into the various frequencies or wavelengths of the radiation. Maxwell’s “classical” theory of electromagnetic oscillators failed to explain the observed brightness distribution. It was left to Max Planck to solve the dilemma by showing that the energy of the oscillators must be quantized, i.e. the energies can not take any value but must change in steps, the size of each step, or quantum, is proportional to the frequency of the oscillator and equal to hv, where h is the Planck constant. With this assumption, Planck derived the brightness distribution of a black body and showed that it is defined by its temperature. Once the temperature of a black body is specified, the Planck law can be used to calculate the intensity of the light emitted by the body as a function of wavelength. Conversely, if the brightness distribution of a radiating body is measured, then, by fitting a Planck curve to it, its temperature can be determined.
The curves illustrated below show that the hotter the body is, the brighter it is at shorter wavelengths. The surface temperature of the sun is 6000 K, and its Planck curve peaks in the visible wavelength range. For bodies cooler than the sun, the peak of the Planck curve shifts to longer wavelengths, until a temperature is reached such that very little radiant energy is emitted in the visible range.
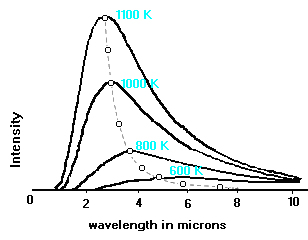
This figure (adapted from Adkins’ “Thermal Physics”) shows several Planck curves for black bodies. The Intensity is in units of energy per unit area per unit solid angle per unit time per unit wavelength interval. The broken line illustrates the variation with wavelength and temperature of the peaks of the curves.
This is a graphical representation of Wien’s law, which states:
 (max) ~ 0.29/T,
(max) ~ 0.29/T,
where  (max) is the wavelength of maximum brightness in cm and T is the absolute temperature of the black body.
(max) is the wavelength of maximum brightness in cm and T is the absolute temperature of the black body.
The human body has a temperature of about 310 K and radiates primarily in the far infrared. If a photograph of a human is taken with a camera sensitive to this wavelength region, we get a “thermal” picture. This picture is courtesy of the Infrared Processing and Analysis Center, Jet Propulsion Laboratory, NASA.
3 K – The Temperature of the Universe
The sun and stars emit thermal radiation covering all wavelengths; other objects in the sky, like the great clouds of gas in the Milky Way, also emit thermal radiation but are much cooler. These objects are best detected by infrared and radio telescopes – telescopes whose detectors are sensitive to the longer wavelengths. In 1965, Arno Penzias and Robert Wilson were conducting a careful calibration of their radio telescope at the Bell Laboratory at Whippany, New Jersey. The found that their receiver showed a “noise” pattern as if it were inside a container whose temperature was 3K – i.e. as if it were in equilibrium with a black body at 3 K. This “noise” seemed to be coming from every direction. Earlier theoretical predictions by George Gamow and other astrophysicists had predicted the existence of a cosmic 3 K background. Penzias’ and Wilson’s discovery was the observational confirmation of the isotropic radiation from the Universe, believed to be a relic of the “Big Bang”. The enormous thermal energy released during the creation of the universe began to cool as the universe expanded. Some 12 billion years later, we are in a universe that radiates like a black body now cooled to 3 K. In 1978 Penzias and Wilson were awarded the Nobel prize in physics for this discovery.
A black body at 3 K emits most of its energy in the microwave wavelength range. Molecules in the earth’s atmosphere absorb this radiation so that from the ground, astronomers cannot make observations in this wavelength region. In 1989 the Cosmic Background Explorer (COBE) satellite, developed by NASA’s Goddard Space Flight Center, was launched to measure the diffuse infrared and microwave radiation from the early universe. One of its instruments, the Far Infrared Absolute Spectrophotometer (FIRAS) compared the spectrum of the cosmic microwave background radiation with a precise blackbody. The cosmic microwave background spectrum was measured with a precision of 0.03% and it fit precisely with a black body of temperature 2.726 K. Even though there are billions of stars in the universe, these precise COBE measurements show that 99.97% of the radiant energy of the Universe was released within the first year after the Big Bang itself and now resides in this thermal 3 K radiation field.
A more detailed explanation of the origin of the microwave background radiation, and its possible anisotropy, may be found here. A new mission selected by NASA is the Microwave Anisotropy Probe (MAP) will measure the small fluctuations in the background radiation and will yield more information on the details of the early universe. The European Space Agency has a similar mission planned.
Summary
The concept of temperature is as fundamental a physical concept as the three fundamental quantities of mechanics – mass, length, and time. Through the study of such practical problems as how to make a highly efficient steam engine, fundamental physical theories emerge, including the concepts of the quantum theory and the two laws of thermodynamics. The second law, with its irreversibility requirement, predicts an inevitable evolution from other forms of energy into heat. It is the second law alone that provides an “arrow” for the concept of time.
We can record events (illustration from Low Temperature Laboratory of Helsinki University of Technology)that cover 18 orders of magnitude in the temperature range, and we have one clearly defined lower limit to the temperature, absolute zero. Because of this 10-with-18-zeros-behind-it range in temperatures, there are many different kinds of thermometers developed to explore it and many different fields of research.
One of the beauties of “publishing” on the web is the interactive element it offers. Joachim Reinhardt has written to point out that the highest temperatures that are accessible on earth (only surpassed by the early stages of the big bang) occur in high-energy collisions of particles (in particular of heavy ions), during which one sees a “fireball” with a temperature of several hundred MeV (which corresponds to a temperature of 10 to the 12th power k). This fireball cools down by expanding and by radiating off particles, mostly pions, quite similar to the thermal black-body radiation. For more information on these phenomena, see the Fermi Lab tutorial.
Thermal physics is a field rich in theoretical and practical applications.
Acknowledgments
I would like to thank Rick Ebert of IPAC for his help in locating some of the infrared files used here and Dave Leisawitz of NASA Goddard for his very careful editing of the article and for his assistance with the COBE results. Joachim Reinhardt generated the pictures of most of the scientists. Thanks to Seth Sharpless for scanning Galen’s picture. Carl Mungan provided advice on low-temperature thermodynamics, and very generously served as an “expert” reviewer.
References
Adkins, C. J. Thermal Physics 1987 Cambridge University Press ISBN 0 521 33715 1
Brain, Marshall How Thermometers Work
Cork, James M. Heat 1942, John Wiley & Sons
Herzfeld, Charles M. Editor, Temperature: Its Measurement and Control in Science and Industry, 1962, Reinhold
National Institutes of Science and Technology: The NIST Reference on Constants, Units, and Uncertainty
Quinn, T. J. Temperature 1990 Academic Press ISBN 0-12-569681-7
Strom, Karen Blackbody Radiation
Texas Center for Superconducitivity An Introduction to High Temperature Superconductivity
University of California, Berkeley Properties of Heat and Matter, Physics Lab
Demonstrations
University of Illinois – Thermodynamic Research Laboratory
University of Oregon Physics Aplets
Weber, Robert L. Heat and Temperature Measurement , 1950, Prentice-Hall, Inc
Zemansky, Mark W. Heat and Thermodynamics 1968, Mc Graw Hill